Introduction - Compound (a.k.a composite) SLAs
Cloud providers publish individuals Service Level Agreements (SLAs) for the individual services they provide. We want to calculate the compound availability of multiple systems based on the following components:
- Azure Traffic Manager: 99.99% or ‘four nines’.
- SQL Azure: 99.99% or ‘four nines’.
- Azure App Service: 99.95% or ‘three nine five’.
When combined together in architectures there is the possibility that any one component could suffer an outage resulting in an overall availability that is not equal to the component services.
Serial Compound Availability

In this example there are three possible failure modes:
- SQL Azure is down
- App Service is down
- Both are down
Serial and Parallel Availability

In this architecture there are a large number of failure modes however principally:
- SQL Server in RegionA is down
- SQL Server in RegionB is down
- App Service in RegionA is down
- App Service in RegionB is down
- Traffic Manager is down
- Combinations of Above
Calculation
We can take that as a math problem with the SLA being the probability of being OK. In this case we can rely on probability rules to get an overall.
For the first case (Serial Compound Availability) the probability that App Service (A) and Sql Service (B) are down at the same time is the product of their probability:
P(A)*P(B) = 0.0005 * 0.0005 = 0,00000025
The probability that one of them is down is the sum of their probability:
P(A)+P(B) = 0.001
When two events are independents the resulting formula to take into account the probability of both being down is:
P(A,B) = P(A) + P(B) - P(A)*P(B) = 0.001 - 0,00000025 = 0,00099975
So the overall SLA would be 1 - 0,00099975 = 0,99900025 which in percent is 99.900025 %
A simplification is the product of the first probability: 0.9995 * 0.9995 = 0,99900025.
Let’s assume that both services were unavailable for one hour today (4,166666% of a day). This gives:
0.04166666 + 0.04166666 - (0.04166666 * 0.04166666) = 0,081597222
So the probability of being OK is 1 - 0.0816 = 0.9184 in percent: 91,84%
24 * 0.0816 = 1.95 h
This is less than the worst case of 2 hours because there’s a chance both are down at the same time.
Keeping that in mind, you may notice the availability for each is 95,84% and 0,958333333 * 0,958333333 = 0,918402778 which is our 91.84% from above (sorry for the full decimals here, but they are needed for the demonstration)
Now for the second case (Serial and Parallel Availability), we’ll start with our compound probability for each region (Sorry I dismissed the change for SQL to keep it reasonable), assuming there’s no independent probability for the region itself and that each region is isolated and as such a DB failure take only its region down.
We have the traffic manager OK probability P(T) = 0.9999 and each app+DB couple with a OK probability P(G) = 0,99900025.
How many regions we have plays a role as we have to apply the product of failure probability just to get the probability of both regions being down at the same time:
0,00099975 * 0,00099975 = 0,0000009995000625 which means an overall availability of at least one region of 99,049375 %.
Now we have the overall regions availability, the product with that of the traffic manager gives us the overall availability of the system:
0.9999 * 0,9999990004999375 = 0,99989900059988750625
The overall availability is 99.989900 %.
Putting it together
For the serial compound availability multiply the probability of each component being available:
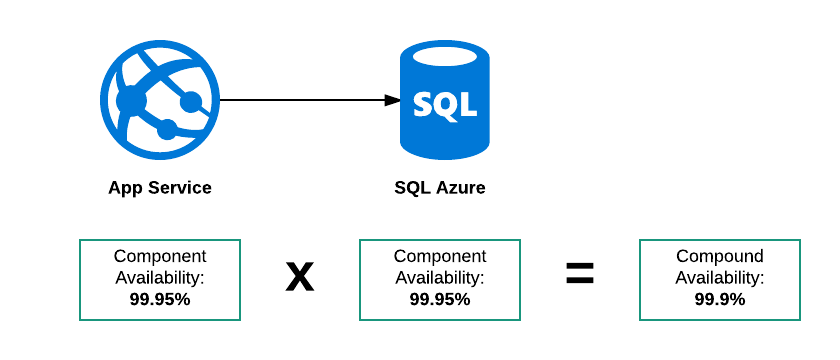
So:
99.95% * 99.95% = 0,99900025% = 99.9%
Calculating it in parallel is a little more complicated as we do need to consider what the percentage unavailability will be:
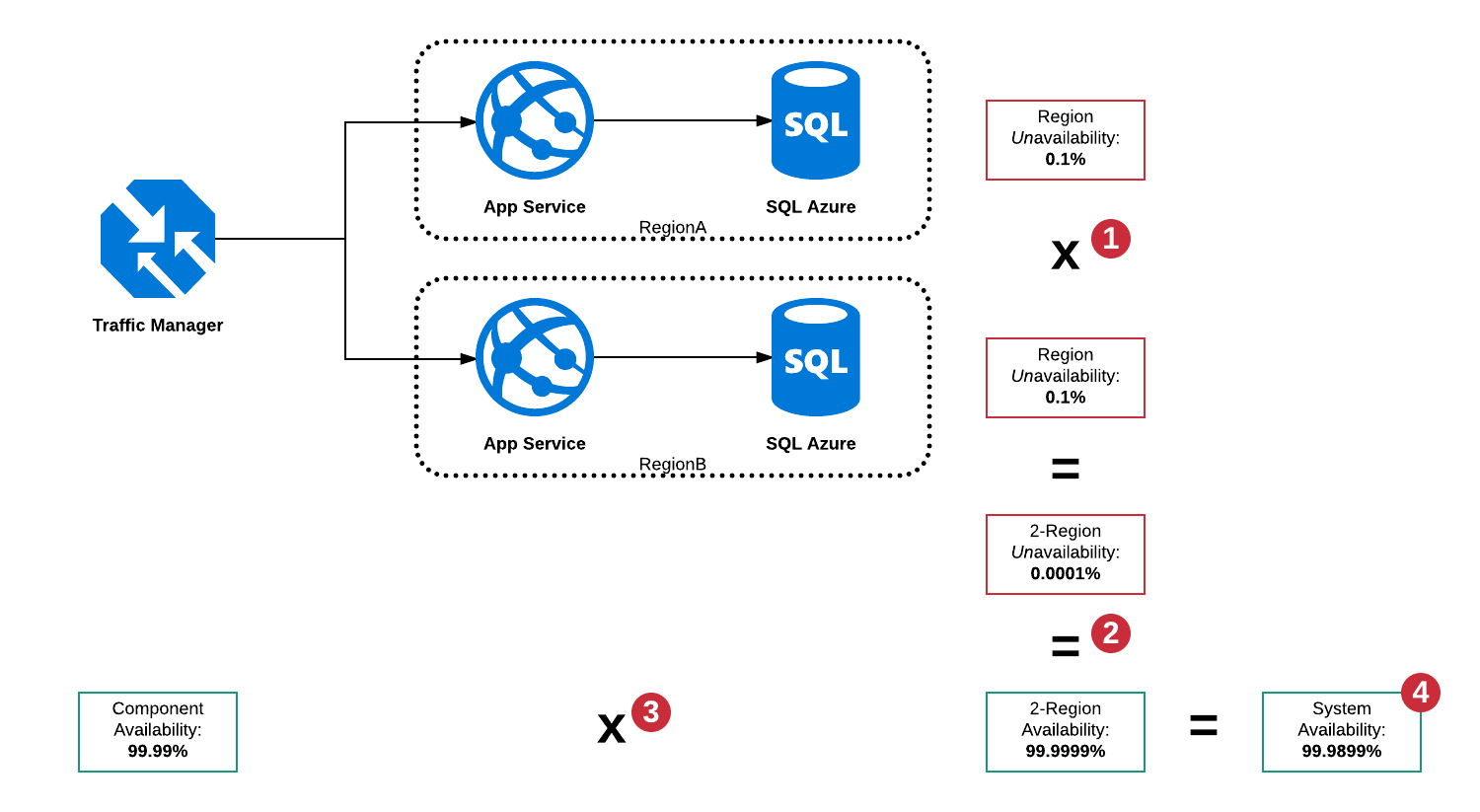
The calculation is done as follows:
- Multiply the unavailability of the two regions together.
0.1% * 0.1% = 0.0001%
- Convert that back to availability
100% - 0.0001% = 99.9999%
- Multiply the Traffic Manager availability by the availability of the two regions.
99.99% * 99.9999% = 99.9899%
- The result is the whole system availability.
99.9899% is close to 99.99%
Here’s a summary of the calculation:
| Component | Availability | Excel Formula |
|---|---|---|
| C1) Traffic Manager | 99,99% | 0,9999 |
| C2) App Service | 99,95% | 0,9995 |
| C3) SQL Azure | 99,95% | 0,9995 |
| C4) Region A | 99,900025% | =C2*C3 |
| C5) Region B | 99,900025% | =C2*C3 |
| C6) Compound | 99,99990% | =1-((1-C4)) * (1-C5)) |
| System | 99,9899% | =C1*C6 |
Another source as explanation is available on Azure’s docs (link courtesy of Raj Rao)
References: